Performance Analysis of Lock Free Hash Table
Paul Chun(pchun1), Mark Fernandez(msfernan)
Summary
We implemented a lock-free hash table using lock-free linked lists. We found out that a lock-free hash-table without memory management improves performance at high thread counts as opposed to a lock-free hash table with locks per list. While a lock-free linked list with memory management shows an improved performance, our lock-free hash table with memory management would need further optimizations to match the performance of a lock-free hash-table without memory management.
Background
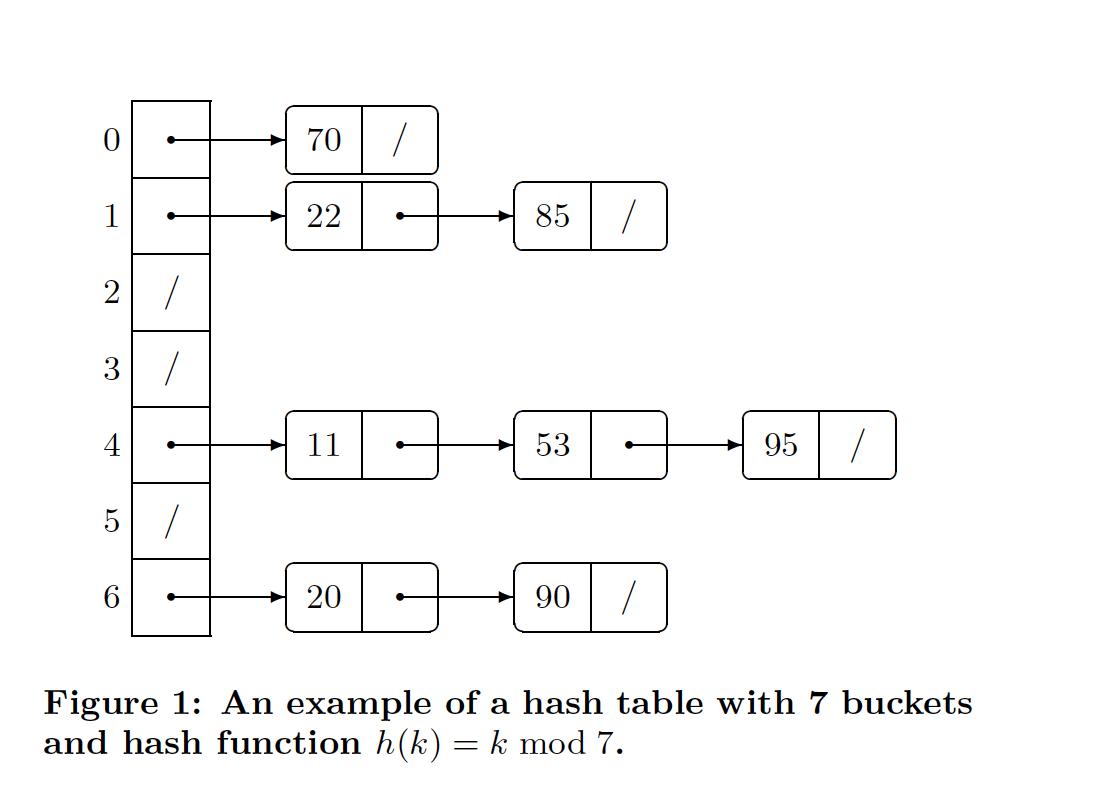
For our application. We implemented a lock-free hash table using separate chaining. The following is a diagram of a hash table. Each key hashes to a specific bucket in our hash table. At each bucket is stored a linked list composed of all the keys that hashed to that specific bucket.
In order to make this hash table lock free, we had to make each of the linked lists that form the hash table lock-free.
There are two ways by which we go about doing this.
The following operations are supported in our hash table.
Insert, Delete and Search make use of a private method find that scans through the linked list and returns true if the node is found at a particular location in the linked list. Find guarantees that the linked list captures a snapshot of the linked list in the prev, curr and next pointers that includes the node (if any) that contains the lowest key value greater than or equal to the input key and its predecessor pointer.
A workload of operations consisting of inserts, deletes and searches is data parallel as different threads can operate on different buckets in the hash table in parallel.
Approach
As mentioned, we decided to develop the project in C++ in order to keep , as it allowed us to create more robust data structures in order to keep the code tidy and readable, whilst allowing the implementation to be efficient and clean.
Machines targeted. Michael used a Michael used a 4-processor (375 MHz604e) IBM PowerPC capable of running 4 superscalar instructions to run his implementation. He had around 16 execution contexts. We developed our on the linux machines that had 12 execution contexts.
We started off by creating a sequential test harness and a linked list with a global lock. Following this moved on to creating a lock-free linked list.
After the lock-free linked list worked with the sequential harness we moved on to creating a parallel test harness. We implemented a barrier class so that we could perform insert operations, synchronize all inserts to complete tests, perform delete operations, synchronize all tests to complete and then perform search operations. Thus we could tell whether the state of our list was what we expected. When we tested for performance however, we removed all the synchronization and interleaved the inserts, deletes and removes.
After this, we moved on to implementing SMR (Safe Memory Reclamation) as a safe memory management technique for the linked list. We do this by associating a shared array of hazard pointers with operating threads. Before deleting from a linked list, we check if any of the hazard pointers from the shared array point to the node we want to delete. If any hazard pointer does point to the node we wish to remove, then we delete the node later. We also delete all the nodes that may not have had a chance to be deleted after the implementation completes. In order to test that each allocated node was deleted, we printed kept a count of each node deleted by each thread and checked if the total nodes deleted matched the total nodes inserted. We also ran valgrind to check for memory errors.
Finally, we implemented a hash table using our linked lists. The hash table had 10000 buckets and since we tested for 10,000 elements, the average load factor was 10.
Results: Description of testing
We measured the amount of time in seconds taken by the CPU to execute a workload of 10,0000 instructions with 4, 8, 16 and 32 threads respectively . The workload was composed of ⅓ insert operations, ⅓ delete operations and ⅓ search operations. The insert, delete and search operations were randomly generated. Each operation is put into a file. When parsing the file, each operations is put into a work queue. The threads pull work from this shared queue and run them. This workload was similar to one of the workloads tested by Michael Maged in his implementation of a lock-free hash table.
This workload was run using the different data structures used in our implementation. We measured this time taken for a lock-free linked list with safe memory management to complete this workload and compared it to the time taken by a linked list with a global lock. We also measured the time taken to complete this workload by a lock-free hash table without memory management to the time taken by a lock-free hash table with safe memory reclamation and the time taken by a hash table with locks per linked list .
The time taken to complete this workload was the average time of 5 runs. In order to speed up the performance, we removed all logging code that we used to check correctness. We used several smaller workloads (such as 1000 operations) but the time taken for each of the data structures was roughly the same. Our implementation requires more optimizations/a different architecture to run larger workloads effectively.
Michael used a 4-processor (375 MHz604e) IBM PowerPC to run his implementation which provided. This processor can issue 4 superscalar instructions so it makes sense that he tested with 16 to 32 threads. We tested and developed on the linux machines which have 12 execution contexts. To get the maximum speedup from our implementation, we should have been running at 12 threads. However, we wanted to be able to compare our results to Michael so we used the same number of threads he did. We will not be to run a workload as large as Michaels as our code will be slower than his due to the machine we are running on. Nevertheless we expected a speedup using our lock-free data structures.
We use the std::hash function provided by the C++ library in order to ensure that the elements are uniformly distributed throughout the hash table.
Results: Description of performance
We found out that our Lock Free Linked List improves performance at high thread counts.
Figure: Lock-Free Linked list with improves performance versus locked.
We also found out that our lock-free hash table without memory management improves performance at high thread counts.
Figure: Lock-Free Hash Table without memory management improves performance
Once we added in the SMR memory management however, we did not get a sufficient improvement over the hash table with locked lists.
Figure: Lock Free hash table with memory management needs further optimization.
Although the performance of the lock-free hash-table with memory management is not as good as the lock-free or even the locked lists case, we know how to make it better. The Safe memory management technique involves associating a shared hazard pointer array with each participating thread. Our algorithm is O(N^M) where N is the length of the hazard pointer array and M is the length of the number of nodes that can remain in the private list before they are freed (M is 2N).
Michael uses an algorithm that is O(NlogN) that we should have implemented. In addition, at high levels of threads counts we have contention that reduces performance. This can be rectified by cache-line padding our hash-table as Michael did. We could also implement atomic compare and swap using assembly as opposed to using the C++ primitives.
References
Michael Maged: High Performance Dynamic Lock-Free Hash Tablesand List-Based Sets, In Proceedings of the 14th Annual ACM Symposium on Parallel Algorithms and Architectures, August 2002
Michael Maged: Safe Memory Reclamation for Dynamic Lock-Free Objects Using Atomic Reads and Writes
http://www.nxp.com/files/32bit/doc/data_sheet/MPC604E.pdf
Work by each student
Equal work was performed by each student.